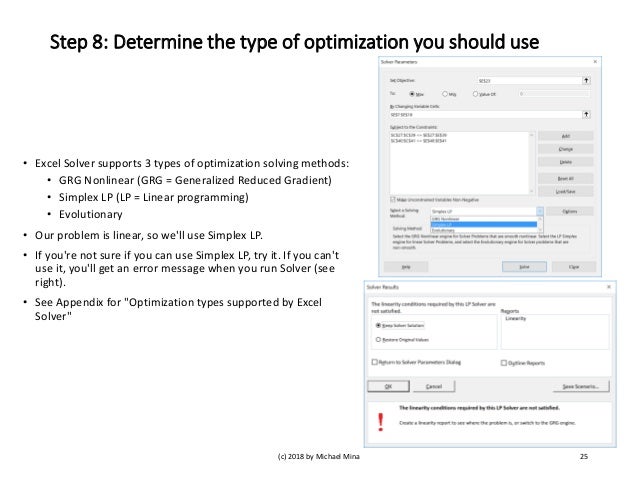
Solving Method” to “SIMPLEX LP” when you are solving a linear program. Finally, click “Solve” for your solution – The Parameters Dialog Box will close and decision variables will change to the optimal solution: Note: because we referenced these cells in all our calculations, the objective function and constraints will.
- Simplex method calculator - Solve the Linear programming problem using Simplex method, step-by-step.
- The kind of report that Excel will create when Solver is finished: When the Simplex LP or GRG Nonlinear Solving method is used, 1 creates an Answer report, 2 creates a Sensitivity report, and 3 creates a Limit report. When the Evolutionary Solving method is used, 1 creates an Answer report, and 2 creates a Population report.
- Matlab implemented simplex method to solve the Linear Programming (LP) problem - li3939108/simplex.
- I would like to reduce an IF statement so that I can use the Simplex LP method but I do not know who to go about doing this. The expresion is below with D14 & E14 being the variable cells =IF.
A model in which the objective function and all of the constraints (other than integer constraints) are linear functions of the decision variables is called a linear programming (LP) problem. (The term “programming” dates from the 1940s and the discipline of “planning and programming” where these solution methods were first used; it has nothing to do with computer programming.) As noted earlier, a linear programming problem is always convex.
If the problem includes integer constraints, it is called an integer linear programming problem. A linear programming problem with some “regular” (continuous) decision variables, and some variables that are constrained to integer values, is called a mixed-integer programming (MIP) problem. Integer constraints are non-convex, and they make the problem far more difficult to solve; see below for details.
A quadratic programming (QP) problem is a generalization of a linear programming problem. Its objective is a convexquadratic function of the decision variables, and all of its constraints must be linear functions of the variables. A problem with linear and convex quadratic constraints, and a linear or convex quadratic objective, is called a quadratically constrained (QCP) problem.
Simplex Lp1020
A model in which the objective function and all of the constraints (other than integer constraints) are smooth nonlinear functions of the decision variables is called a nonlinear programming (NLP) or nonlinear optimization problem. If the problem includes integer constraints, it is called an integer nonlinear programming problem. A model in which the objective or any of the constraints are non-smooth functions of the variables is called a non-smooth optimization (NSP) problem.
Load the Solver Add-in | Formulate the Model | Trial and Error | Solve the Model
Excel includes a tool called solver that uses techniques from the operations research to find optimal solutions for all kind of decision problems.
Load the Solver Add-in
To load the solver add-in, execute the following steps.
1. On the File tab, click Options.
2. Under Add-ins, select Solver Add-in and click on the Go button.
3. Check Solver Add-in and click OK.
Simplex Lp1010
4. You can find the Solver on the Data tab, in the Analyze group.
Formulate the Model
The model we are going to solve looks as follows in Excel.
1. To formulate this linear programming model, answer the following three questions.
a. What are the decisions to be made? For this problem, we need Excel to find out how much to order of each product (bicycles, mopeds and child seats).
b. What are the constraints on these decisions? The constrains here are that the amount of capital and storage used by the products cannot exceed the limited amount of capital and storage (resources) available. For example, each bicycle uses 300 units of capital and 0.5 unit of storage.
Simplex Lp1000
c. What is the overall measure of performance for these decisions? The overall measure of performance is the total profit of the three products, so the objective is to maximize this quantity.
Simplex Lp
2. To make the model easier to understand, create the following named ranges.
| Range Name | Cells |
|---|---|
| UnitProfit | C4:E4 |
| OrderSize | C12:E12 |
| ResourcesUsed | G7:G8 |
| ResourcesAvailable | I7:I8 |
| TotalProfit | I12 |
Simplex Lp1000 Parts
3. Insert the following three SUMPRODUCT functions.
Explanation: The amount of capital used equals the sumproduct of the range C7:E7 and OrderSize. The amount of storage used equals the sumproduct of the range C8:E8 and OrderSize. Total Profit equals the sumproduct of UnitProfit and OrderSize.
Trial and Error
With this formulation, it becomes easy to analyze any trial solution.
For example, if we order 20 bicycles, 40 mopeds and 100 child seats, the total amount of resources used does not exceed the amount of resources available. This solution has a total profit of 19000.
It is not necessary to use trial and error. We shall describe next how the Excel Solver can be used to quickly find the optimal solution.
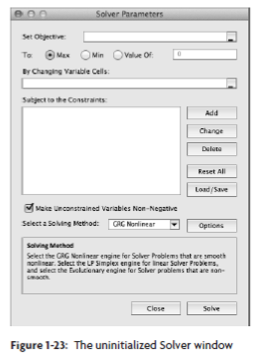
Solve the Model
To find the optimal solution, execute the following steps.
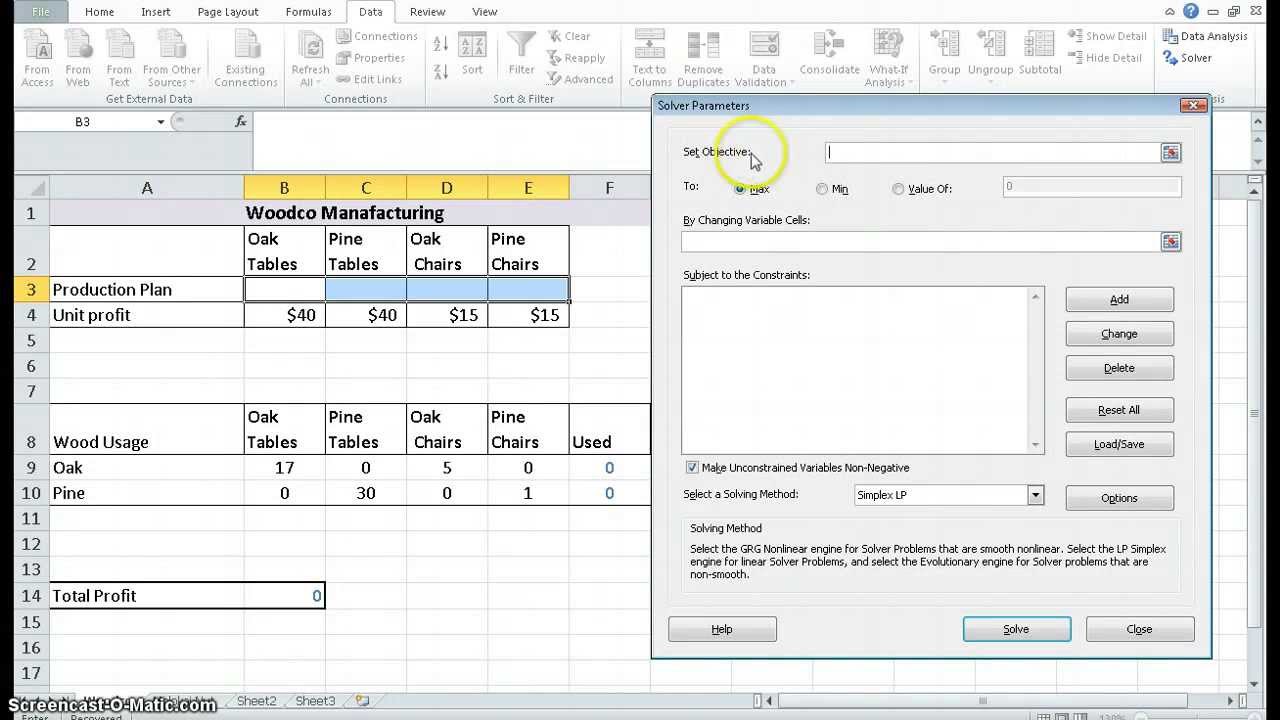
1. On the Data tab, in the Analyze group, click Solver.
Enter the solver parameters (read on). The result should be consistent with the picture below.
You have the choice of typing the range names or clicking on the cells in the spreadsheet.
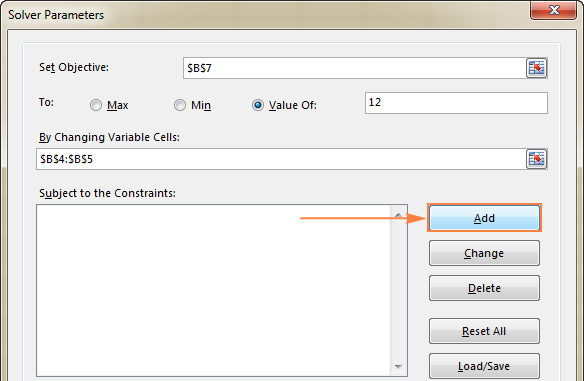
2. Enter TotalProfit for the Objective.
3. Click Max.
4. Enter OrderSize for the Changing Variable Cells.
5. Click Add to enter the following constraint.
6. Check 'Make Unconstrained Variables Non-Negative' and select 'Simplex LP'.
Kaba Lp1000 Template
7. Finally, click Solve.
Result:
The optimal solution:
Conclusion: it is optimal to order 94 bicycles and 54 mopeds. This solution gives the maximum profit of 25600. This solution uses all the resources available.
